Enveloping Measures

Generally speaking, chance-constrained programming seeks an optimal solution in which the requirement(s), convoluted by uncertainties arising from operations, is (are) satisfied with a certain probability. However, there are several issues when using this approach.

• Once a chance-constraint is violated, there is no limit on how worse it can be. (See here for details.)
• To avoid the first problem, a long list of chance-constraints can be used but the process is not scalable.
• Most importantly, chance-constrained problems are difficult to optimize in general.

This project, among other things, is to address the above problems by introducing an efficient solution method. Notice that this can be easily extended to distributionally robust problems. First, denote the decision variables and the feasible set as \(\mathbf{x}\) and \(\mathcal{X}\) respectively.

1. Select a utility function \(u(\cdot)\) according to your risk appetite.
2. Define a (random) payoff function \(f(\mathbf{x}, \mathbf{\tilde{z}})\) (e.g., \(\mathbf{x}^T \mathbf{\tilde{z}}\)). We assume a positive value is preferred.
3. Obtain the value of \(\rho^\ast\) by solving the optimization problem defined on the right, i.e., \(\rho^\ast := \inf \{k > 0 ~:~ \mathbb{E}[u(-f(\mathbf{x}, \mathbf{\tilde{z}}) / k)] \leq 1, \mathbf{x} \in \mathcal{X} \}\). We call this a utility-based CREM.
4. Plug \(\rho^\ast\) and \(u\) into the inequality, \(\mathbb{P}(-f(\mathbf{x}, \mathbf{\tilde{z}}) > \phi) \leq 1 / u(\phi / \rho^\ast)\), which holds for all \(\phi > 0\). Voila! This is the probability bound that holds at all loss levels (i.e., how unfavorable an outcome is) and can be thought of as an infinite list of chance-constraints!

To have a concrete idea of how reliable your optimal solution is, you can tabulate the results or plot \(1 / u(\phi / \rho^\ast)\) against \(\phi\) (see the GIF below). Consider changing \(u\) (or even \(f\) and \(\mathcal{X}\)) if you are not so happy with the results.

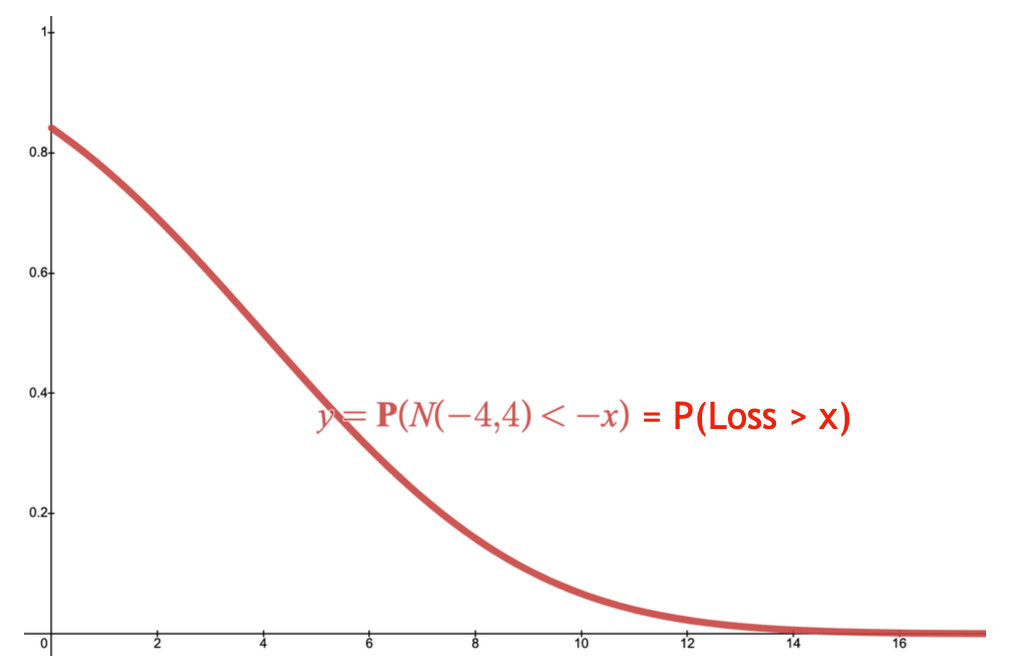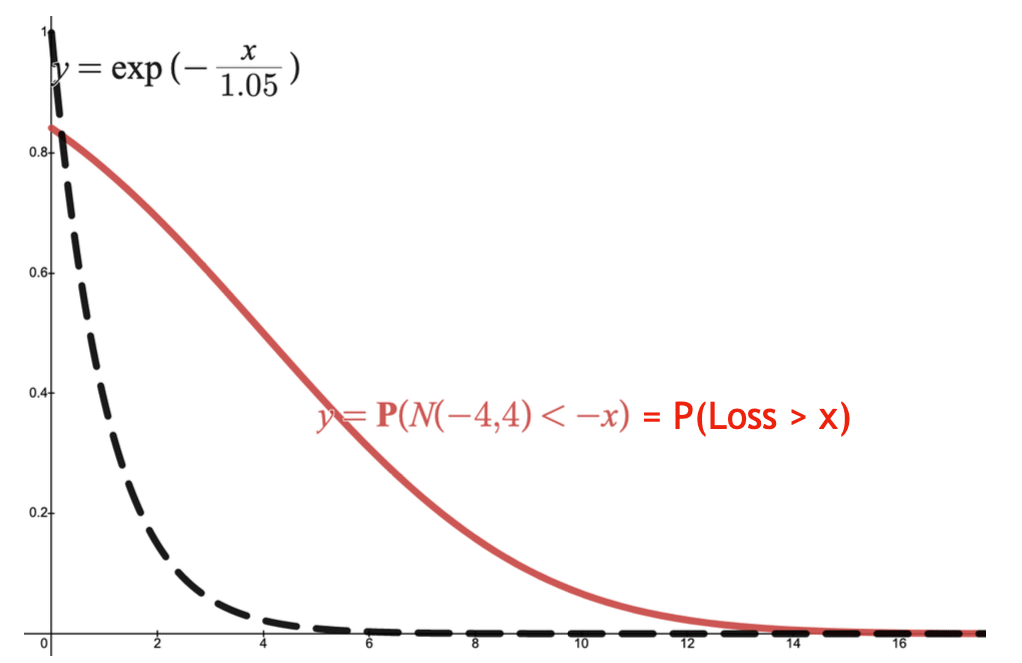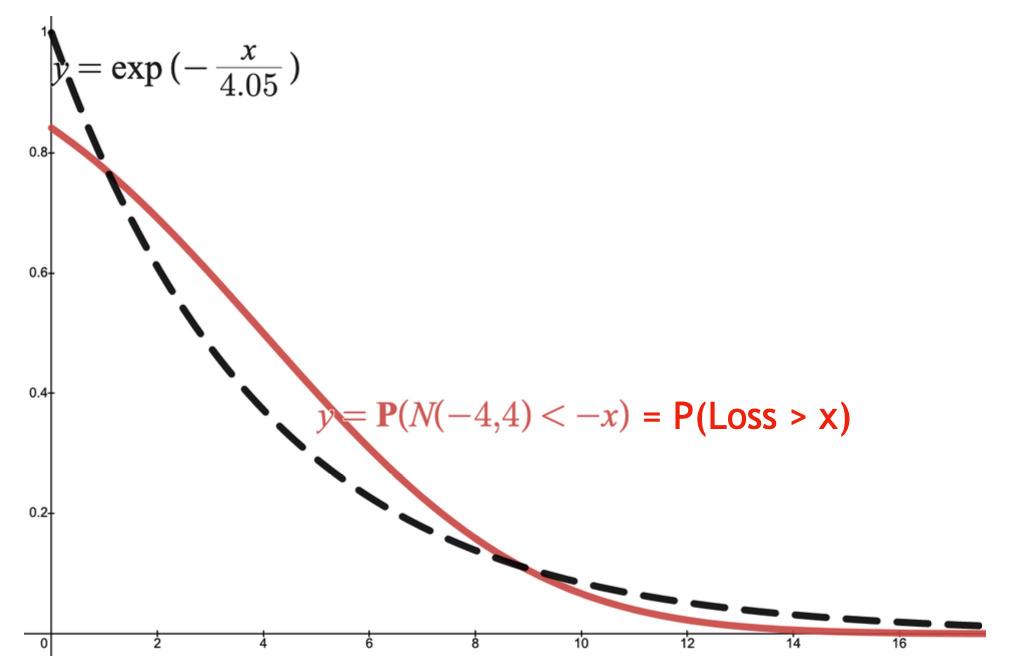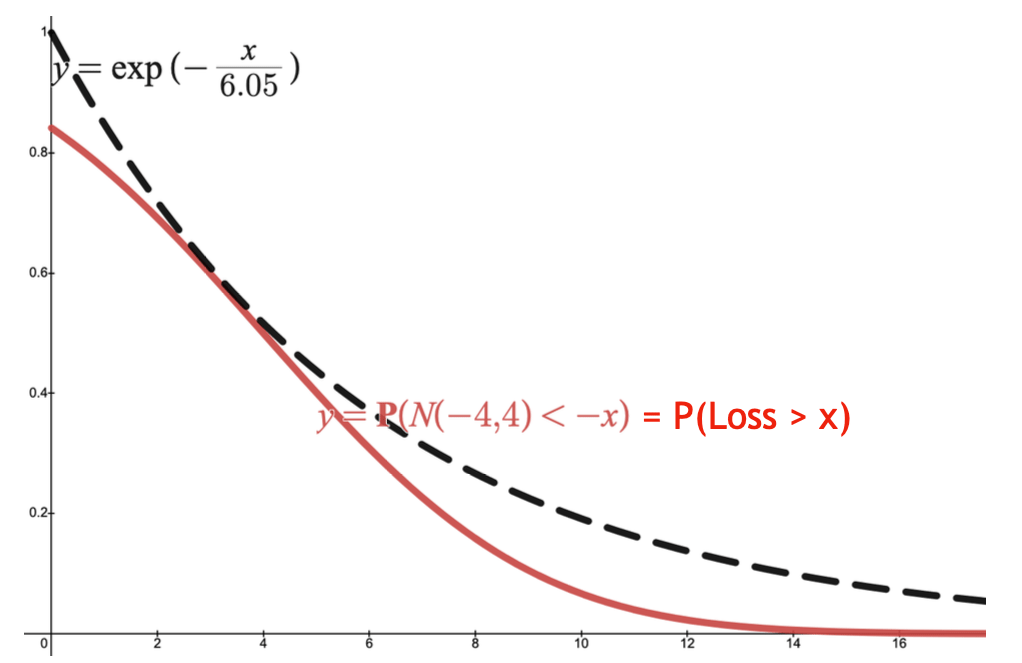
The graph gives an intuitive interpretation of utility-based CREMs. The vertical axis represents the probability levels, whereas the horizontal axis indicates the loss levels. Here, we define \(u(x) = \exp(x)\). The CDF of a loss is plotted in a solid red curve.

• If \(k\) is “too big” or “too small”, the probability bound (i.e., the dotted black curve) is too loose or it simply fails to hold.
• So we need to find a “just right” value for \(k\) so that the black curve is “just above” the red one, or more precisely,
  • it is the lowest among the same family of dotted black curves and
  • is above the red line.